pdf 파일 : 도형의 이동 기출문제 모음
1. 2016년 3월학평 가형 10 번(고2)
좌표평면에서 원 \((x+1)^2+(y+2)^2=9\) 를 \(x\) 축의 방향 으로 3 만큼, \(y\) 축의 방향으로 \(a\) 만큼 평행이동한 원을 \(C\) 라 하자. 원 \(C\) 의 넓이가 직선 \(3 x+4 y-7=0\) 에 의하 여 이등분되도록 하는 상수 \(a\) 의 값은? (3점)
(1) \(\frac{1}{4}\)
(2) \(\frac{3}{4}\)
(3) \(\frac{5}{4}\)
(4) \(\frac{7}{4}\)
(5) \(\frac{9}{4}\)

원 \(C\) 의 방정식은
\[
\{(x-3)+1\}^2+\{(y-a)+2\}^2=9
\]
\[
(x-2)^2+(y-a+2)^2=9
\]
원 \(C\) 의 넓이가 직선 \(3 x+4 y-7=0\) 에 의하여 이등 분되려면 원 \(C\) 의 중심이 직선 \(3 x+4 y-7=0\) 위에 있어야 한다.
원 \(C\) 의 중심의 좌표가 \((2, a-2)\) 이므로
\[
\begin{aligned}
& 3 \times 2+4(a-2)-7=0 \text { 에서 } \\
& a=\frac{9}{4}
\end{aligned}
\]
2. 2018년 11월학평 15번(고1)
좌표평면에서 직선 \(3 x+4 y+17=0\) 을 \(x\) 축의 방향으로 \(n\) 만큼 평행이동한 직선이 원 \(x^2+y^2=1\) 에 접할 때, 자연수 \(n\) 의 값은? (4점)
(1) 1
(2) 2
(3) 3
(4) 4
(5) 5

직선 \(3 x+4 y+17=0\) 을 \(x\) 축의 방향으로 \(n\) 만큼 평행이동한 직선의 방정식은
\[
3(x-n)+4 y+17=0
\]
직선 \(3 x+4 y-3 n+17=0\) 이 원 \(x^2+y^2=1\) 에 접하므로 원의 중심 \((0,0)\) 과
직선 \(3 x+4 y-3 n+17=0\) 사이의 거리가 1 이다.
\[
\begin{aligned}
& \frac{|-3 n+17|}{\sqrt{3^2+4^2}}=1 \text { 에서 } \\
& -3 n+17=5 \text { 또는 }-3 n+17=-5 \\
& 그러므로 n=4 \text { 또는 } n=\frac{22}{3}
\end{aligned}
\]
\(n\) 은 자연수이므로 \(n=4\)
3. 2011년 3월학평 27번(고2)
좌표평면에서 포물선 \(y=x^2-2 x\) 를 포물선 \(y=x^2-12 x+30\) 으로 옮기는 평행이동에 의하여 직선 \(l: x-2 y=0\) 이 직선 \(l^{\prime}\) 으로 옮겨진다. 두 직선 \(l, l^{\prime}\) 사이의 거리를 \(d\) 라 할 때, \(d^2\) 의 값을 구하시오. (4점)

포물선 \(y=x^2-2 x\) 를 \(x\) 축 방향으로 \(m\) 만큼, \(y\) 축 방 향으로 \(n\) 만큼 평영이봉하면
\[
y-n=(x-m)^2-2(x-m)
\]
정리하면 \(y=x^2-2(m+1) x+m^2+2 m+n\)
이 포물선이 \(y=x^2-12 x+30\) 과 일치하므로 \(m=5, n=-5\) 이다.
직선 \(l: x-2 y=0\) 을 \(x\) 축 방향으로 5 만큼, \(y\) 축 방향 으로 -5 만큼 평행이봉하면 \((x-5)-2(y+5)=0\) 이므 로 직선 \(l: x-2 y-15=0\) 이다.
따라서 두 직선 \(l, i\) 사이의 거리 \(d\) 는 직선 \(x-2 y=0\) 위의 점 \((0,0)\) 과 직선 \(x-2 y-15=0\) 사이 의 거리와 같다.
\[
\begin{aligned}
& d=\frac{15}{\sqrt{5}}=3 \sqrt{5} \\
& 그러므로 d^2=45
\end{aligned}
\]
4. 2019년 9월학평 15번(고1)
원 \(C_1: x^2+y^2=2\) 를 \(x\) 축의 방향으로 \(k\) 만큼, \(y\) 축의 방향으로 \(k\) 만큼 평행이동한 원을 \(C_2\) 라 하자. 점 \(\mathrm{A}(1,1)\) 에서 원 \(C_2\) 에 그은 두 접선이 서로 수직일 때, 상수 \(k\) 의 값은? (단, \(k>2\) ) (4점)
(1) \(1+\sqrt{2}\)
(2) \(2+\sqrt{2}\)
(3) \(1+2 \sqrt{2}\)
(4) \(3+\sqrt{2}\)
(5) \(2+2 \sqrt{2}\)
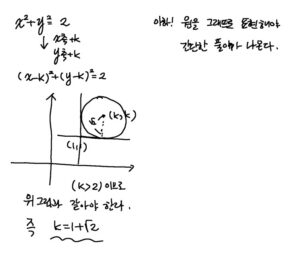
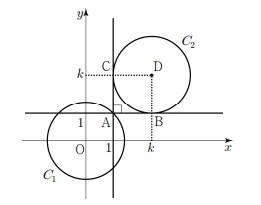
점 \(\mathrm{A}(1,1)\) 에서 원 \(C_2\) 에 그은 두 접선이 원 \(C_2\) 와 만나는 점을 각각 \(\mathrm{B}, \mathrm{C}\) 라 하고, 원 \(C_2\) 의 중심을 \(\mathrm{D}(k, k)\) 라 하자.
사각형 \(\mathrm{ABDC}\) 는 한 변의 길이가 \(\sqrt{2}\) 인 정사각형이다.
\(k>2\) 이므로 \(k=1+\sqrt{2}\)
5. 2018년 9월학평 27번(고1)
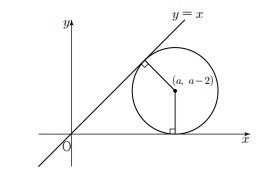
원 \((x-a)^2+(y-a)^2=b^2\) 을 \(y\) 축의 방향으로 -2 만큼 평행이동한 도형이 직선 \(y=x\) 와 \(x\) 축에 동시에 접할 때, \(a^2-4 b\) 의 값을 구하시오.
(단, \(a>2, b>0\) )
(4점)

원 \((x-a)^2+(y-a)^2=b^2\) 을 \(y\) 축의 방향으로 -2 만큼 평행이동한 도형은 중심이 \((a, a-2)\), 반지름이 \(a-2(a>2)\) 인 원이다.
또한 이 원이 직선 \(y=x\) 와 접하므로
\[
\begin{aligned}
& \frac{|a-(a-2)|}{\sqrt{1^2+(-1)^2}}=a-2 \\
& a=2+\sqrt{2} \\
& b=a-2=\sqrt{2}
\end{aligned}
\]
따라서 \(a^2-4 b=6\)
6. 2019년 9월학평 19번(고1)
좌표평면 위에 세 점 \(\mathrm{A}(0,9), \mathrm{B}(-9,0), \mathrm{C}(9,0)\) 이 있다. 실수 \(t(0<t<18)\) 에 대하여 세 점 \(\mathrm{O}, \mathrm{A}, \mathrm{B}\) 를 \(x\) 축의 방향으로 \(t\) 만큼 평행이동한 점을 각각 \(\mathrm{O}^{\prime}, \mathrm{A}^{\prime}\), \(\mathrm{B}^{\prime}\) 이라 하자. 삼각형 \(\mathrm{OCA}\) 의 내부와 삼각형 \(\mathrm{O}^{\prime} \mathrm{A}^{\prime} \mathrm{B}^{\prime}\) 의 내부의 공통부분의 넓이를 \(S(t)\) 라 할 때, \(S(t)\) 의 최댓 값은?
(단, \(\mathrm{O}\) 는 원점이다.) (4점)
(1) 21
(2) 24
(3) 27
(4) 30
(5) 33
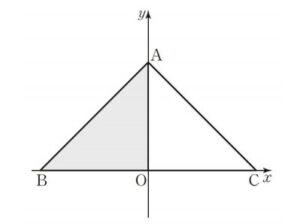

(i) \(0<t<9\) 일 때,
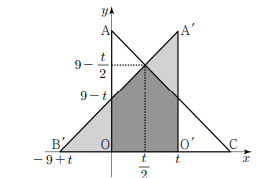
\[
\begin{aligned}
S(t) & =2 \times \frac{1}{2} \times\left(9-t+9-\frac{t}{2}\right) \times \frac{t}{2} \\
& =\frac{3}{4} t(12-t)=-\frac{3}{4}(t-6)^2+27
\end{aligned}
\]
따라서 \(t=6\) 일 때, \(S(t)\) 의 최댓값은 27
(ii) \(9 \leq t<18\) 일 때,
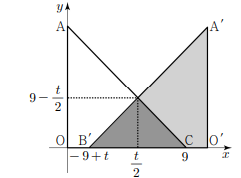
\[
S(t)=\frac{1}{2} \times(18-t) \times\left(9-\frac{t}{2}\right)=\frac{1}{4}(t-18)^2
\]
따라서 \(t=9\) 일 때, \(S(t)\) 의 최댓값은 \(\frac{81}{4}\)
(i), (ii)에서 \(S(t)\) 의 최댓값은 27
7. 2019년 11월학평 27번(고1)
좌표평면 위에 두 점 \(\mathrm{A}(1,2), \mathrm{B}(2,1)\) 이 있다. \(x\) 축 위의 점 \(\mathrm{C}\) 에 대하여 삼각형 \(\mathrm{ABC}\) 의 둘레의 길이의 최 솟값이 \(\sqrt{a}+\sqrt{b}\) 일 때, 두 자연수 \(a, b\) 의 합 \(a+b\) 의 값을 구하시오.
(단, 점 \(\mathrm{C}\) 는 직선 \(\mathrm{AB}\) 위에 있지 않다.) (4점)

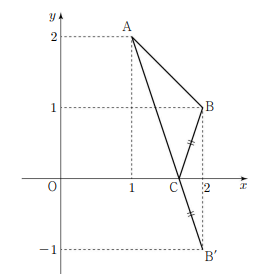
삼각형 \(\mathrm{ABC}\) 의 둘레의 길이는 \(\overline{\mathrm{AC}}+\overline{\mathrm{CB}}+\overline{\mathrm{BA}}\) 점 \(\mathrm{B}(2,1)\) 을 \(x\) 축에 대하여 대칭이동한 점을 \(\mathrm{B}^{\prime}\) 이라 하면 점 \(\mathrm{B}^{\prime}\) 의 좌표는 \((2,-1)\) 이다.
\(\overline{\mathrm{AC}}+\overline{\mathrm{CB}}=\overline{\mathrm{AC}}+\overline{\mathrm{CB}^{\prime}} \geq \overline{\mathrm{AB}^{\prime}}\) 이고
\(\overline{\mathrm{BA}}=\sqrt{2}, \overline{\mathrm{AB}^{\prime}}=\sqrt{10}\) 이므로
삼각형 \(\mathrm{ABC}\) 의 둘레의 길이의 최솟값은 \(\sqrt{2}+\sqrt{10}\)
따라서 \(a+b=12\)
8. 2006년 5월학평 나형 12번(고2)
두 점 \(\mathrm{A}(4,1), \mathrm{B}(2,5)\) 와 \(x\) 축 위의 임의의 점 \(\mathrm{P}, y\) 축 위의 임의의 점 \(\mathrm{Q}\) 에 대하여 사각형 \(\mathrm{APQB}\) 의 둘레 의 길이가 최소일 때, 직선 \(\mathrm{PQ}\) 의 기울기는? (4점)
(1) \(-\frac{5}{3}\)
(2) \(-\frac{4}{3}\)
(3) -1
(4) \(-\frac{2}{3}\)
(5) \(-\frac{1}{3}\)
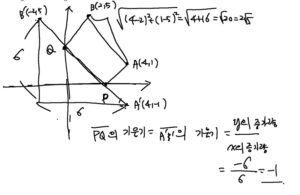
9. 2020년 9월학평 13번(고1)
05. 원 \((x-6)^2+(y+3)^2=4\) 위의 점 \(\mathrm{P}\) 와 \(x\) 축 위의 점 \(\mathrm{Q}\) 가 있다. 점 \(\mathrm{A}(0,-5)\) 에 대하여 \(\overline{\mathrm{AQ}}+\overline{\mathrm{QP}}\) 의 최솟값은? (3점)
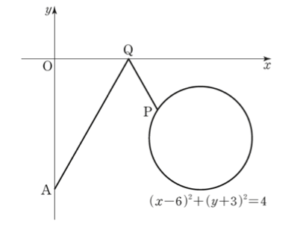
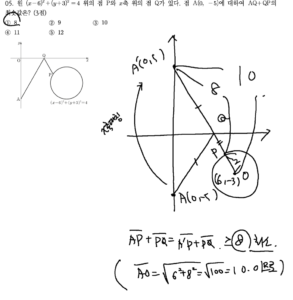
점 \(\mathrm{A}(0,-5)\) 를 \(x\) 축에 대하여 대칭이동한 점을 \(\mathrm{A}^{\prime}\) 이라 하면 \(\mathrm{A}^{\prime}(0,5)\)
원의 중심을 \(\mathrm{C}\) 라 하면 \(\mathrm{C}(6,-3)\)
\[
\begin{aligned}
& \overline{\mathrm{AQ}}=\overline{\mathrm{A}^{\prime} \mathrm{Q}}, \overline{\mathrm{A}^{\prime} \mathrm{C}}=\sqrt{(6-0)^2+(-3-5)^2}=10 \\
& \overline{\mathrm{AQ}}+\overline{\mathrm{QP}}=\overline{\mathrm{A}^{\prime} \mathrm{Q}}+\overline{\mathrm{QP}} \geq \overline{\mathrm{A}^{\prime} \mathrm{P}} \geq \overline{\mathrm{A}^{\prime} \mathrm{C}}-2=8 \\
& \text { 따라서 } \overline{\mathrm{AQ}}+\overline{\mathrm{QP}} \text { 의 최솟값은 } 8
\end{aligned}
\]
10. 2015년 11월학평 27번(고1)
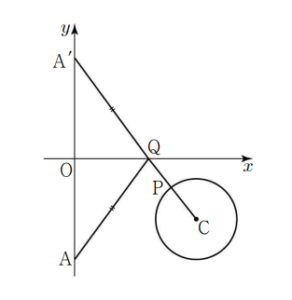
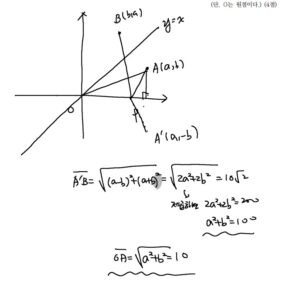
좌표평면에서 제 1 사분면 위의 점 \(\mathrm{A}\) 를 \(y=x\) 에 대하여 대칭이동시킨 점을 \(\mathrm{B}\) 라 하자. \(x\) 축 위의 점 \(\mathrm{P}\) 에 대하 여 \(\overline{\mathrm{AP}}+\overline{\mathrm{PB}}\) 의 최솟값이 \(10 \sqrt{2}\) 일 때, 선분 \(\mathrm{OA}\) 의 길 이를 구하시오.
(단, \(\mathrm{O}\) 는 원점이다.) (4점)
11. 2006년 11월학평 20번(고1)
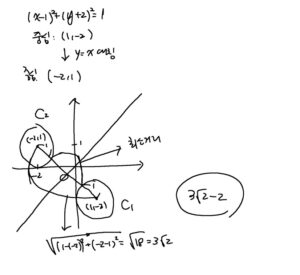
원 \(C_1: x^2-2 x+y^2+4 y+4=0\) 을 직선 \(y=x\) 에 대하 여 대칭이동한 원을 \(C_2\) 라 하자. \(C_1\) 위의 임의의 점 \(\mathrm{P}\) 와 \(C_2\) 위의 임의의 점 \(\mathrm{Q}\) 에 대하여 두 점 \(\mathrm{P}, \mathrm{Q}\) 사이 의 최소 거리는? (4점)
(1) \(2 \sqrt{3}-2\)
(2) \(2 \sqrt{3}+2\)
(3) \(3 \sqrt{2}-2\)
(4) \(3 \sqrt{2}+2\)
(5) \(3 \sqrt{3}-2\)
\[
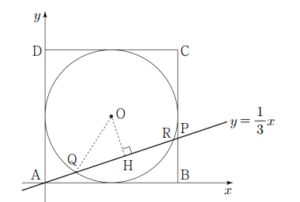
\overline{\mathrm{AB}}: \overline{\mathrm{BP}}=3: 1
\] 직선 \(\mathrm{AP}\) 는 기울기가 \(\frac{1}{3}\) 이고 원점을 지나므로
직선 \(\mathrm{AP}\) 의 방정식은 \(y=\frac{1}{3} x\) 이다.
원의 중심을 \(\mathrm{O}\) 라 하면 정사각형 \(\mathrm{ABCD}\) 의 한 변의 길이가 10 이므로 \(\mathrm{O}(5,5)\) 이고, \(\overline{\mathrm{OQ}}=5\)
점 \(\mathrm{O}(5,5)\) 에서 직선 \(x-3 y=0\) 에 내린 수선의 발을 \(\mathrm{H}\) 라 하면
\[
\begin{aligned}
& \overline{\mathrm{OH}}=\frac{|5-15|}{\sqrt{1^2+3^2}}=\frac{10}{\sqrt{10}}=\sqrt{10} \\
& 그러므로 \overline{\mathrm{QH}}=\sqrt{15}
\end{aligned}
\] 따라서 \(\overline{\mathrm{QR}}=2 \sqrt{15}\)
12. 2017년 9월학평 15번(고1)
직선 \(y=-\frac{1}{2} x-3\) 을 \(x\) 축의 방향으로 \(a\) 만큼 평행이동 한 후 직선 \(y=x\) 에 대하여 대칭이동한 직선을 \(l\) 이라 하자. 직선 \(l\) 이 원 \((x+1)^2+(y-3)^2=5\) 와 접하도록 하는 모든 상수 \(a\) 의 값의 합은? (4점)
(1) 14
(2) 15
(3) 16
(4) 17
(5) 18

직선 \(y=-\frac{1}{2} x-3\) 을 \(x\) 축의 방향으로 \(a\) 만큼 평행이동한 직선은 \(y=-\frac{1}{2}(x-a)-3\) 이고 이를 직선 \(y=x\) 에 대하여 대칭이동한 직선 \(l\) 은 \(x=-\frac{1}{2}(y-a)-3\), 즉 \(2 x+y-a+6=0\) 직선 \(l\) 이 원에 접하므로 원의 중심 \((-1,3)\) 에서 직선 \(l\) 까지의 거리 \(d=\frac{|-2+3-a+6|}{\sqrt{5}}=\sqrt{5}\) 따라서 \(a=2,12\) 이므로 모든 \(a\) 값의 합은 14
13, 2021년 3월학평 15번(고2)
좌표평면에서 세 점 \(\mathrm{A}(1,3), \mathrm{B}(\mathrm{a}, 5), \mathrm{C}(\mathrm{b}, \mathrm{c})\) 가 다 음 조건을 만족시킨다.
(가) 두 직선 \(\mathrm{OA}, \mathrm{OB}\) 는 서로 수직이다.
(나) 두 점 \(\mathrm{B}, \mathrm{C}\) 는 직선 \(y=x\) 에 대하여 서로 대 칭이다.
직선 \(\mathrm{AC}\) 의 \(y\) 절편은? (단, \(\mathrm{O}\) 는 원점이다.) (4점)
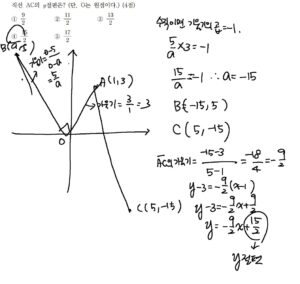
직선 \(\mathrm{OA}\) 의 기울기는 \(\frac{3-0}{1-0}=3\) 이고 직선 \(\mathrm{OB}\) 의 기울 기를 \(m\) 이라 하면 두 직선 \(\mathrm{OA}, \mathrm{OB}\) 가 서로 수직이므 로 두 직선의 기울기의 곱이 -1 이어야 한다.
\[
3 m=-1
\]
에서
\[
m=-\frac{1}{3}
\]
즉, \(a \neq 0\) 이고 직선 \(\mathrm{OB}\) 의 기울기는
\[
\begin{aligned}
& \frac{5-0}{a-0}=\frac{5}{a}=-\frac{1}{3} \\
& a=-15
\end{aligned}
\]
점 \(\mathrm{B}\) 의 좌표는 \((-15,5)\)
또한 두 점 \(\mathrm{B}, \mathrm{C}\) 가 직선 \(y=x\) 에 대하여 서로 대칭
이므로
\[
b=5, c=-15
\]
즉, \(\mathrm{A}(1,3), \mathrm{C}(5,-15)\) 이므로 직선 \(\mathrm{AC}\) 의 방정식은
\[
\begin{aligned}
& y-3=\frac{-15-3}{5-1} \times(x-1) \\
& y=-\frac{9}{2} x+\frac{15}{2}
\end{aligned}
\]
따라서 직선 \(\mathrm{AC}\) 의 \(y\) 절편은 \(\frac{15}{2}\) 이다.
14. 2019년 9월학평 16번(고1)
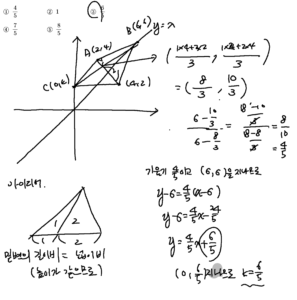
좌표평면 위에 두 점 \(\mathrm{A}(2,4), \mathrm{B}(6,6)\) 이 있다. 점 \(\mathrm{A}\) 를 직선 \(y=x\) 에 대하여 대칭이동한 점을 \(\mathrm{A}^{\prime}\) 이라 하 자. 점 \(\mathrm{C}(0, k)\) 가 다음 조건을 만족시킬 때, \(k\) 의 값은? (4점)
(가) \(0<k<3\)
(나) 삼각형 \(\mathrm{A}^{\prime} \mathrm{BC}\) 의 넓이는 삼각형 \(\mathrm{ACB}\) 의 넓이의 2 배이다.
(1) \(\frac{4}{5}\)
(2) 1
(3) \(\frac{6}{5}\)
(4) \(\frac{7}{5}\)
(5) \(\frac{8}{5}\)
15. 2015년 3월학평 나형 18번(고2)
좌표평면에서 두 점 \(\mathrm{A}(4, a), \mathrm{B}(2,1)\) 을 직선 \(y=x\) 에 대하여 대칭이동한 점을 각각 \(\mathrm{A}^{\prime}, \mathrm{B}^{\prime}\) 이라 하고, 두 직선 \(\mathrm{AB}, \mathrm{A}^{\prime} \mathrm{B}^{\prime}\) 의 교점을 \(\mathrm{P}\) 라 하자. 두 삼각형 \(\mathrm{APA}^{\prime}, \mathrm{BPB}^{\prime}\) 의 넓이의 비가 \(9: 4\) 일 때, \(a\) 의 값은? (단, \(a>4\) ) (4점)
(1) 5
(2) \(\frac{11}{2}\)
(3) 6
(4) \(\frac{13}{2}\)
(5) 7
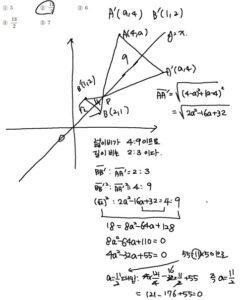
직선 \(\mathrm{AB}\) 의 방정식은 \(y=\frac{1}{2} x+3\)
직선 \(\mathrm{AB}\) 를 직선 \(y=x\) 에 대하여 대칭이동한
직선 \(\mathrm{A}^{\prime} \mathrm{B}\) 의 방정식은 \(y=2 x-6\)
점 \(\mathrm{C}\) 와 직선 \(\mathrm{A}^{\prime} \mathrm{B}\) 사이의 거리는
점 \(\mathrm{C}\) 와 직선 \(\mathrm{AB}\) 사이의 거리의 2 배이다.
\[
\begin{aligned}
& \frac{|-k-6|}{\sqrt{2^2+(-1)^2}}=\frac{|-2 k+6|}{\sqrt{1^2+(-2)^2}} \times 2 \\
& 0<k<3 \text { 이므로 } k+6=2(-2 k+6) \\
& \text { 따라서 } k=\frac{6}{5}
\end{aligned}
\]
16. 2016년 3월학평 가형 27번(고2)
그림과 같이 좌표평면에서 두 점 \(\mathrm{A}(2,0), \mathrm{B}(1,2)\) 를 직선 \(y=x\) 에 대하여 대칭이동한 점을 각각 \(\mathrm{C}, \mathrm{D}\) 라 하 자. 삼각형 \(\mathrm{OAB}\) 및 그 내부와 삼각형 \(\mathrm{ODC}\) 및 그 내 부의 공통부분의 넓이를 \(S\) 라 할 때, \(60 S\) 의 값을 구하 시오. (단, \(\mathrm{O}\) 는 원점이다.)
(4점)
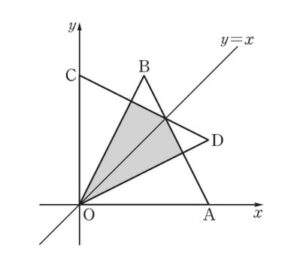
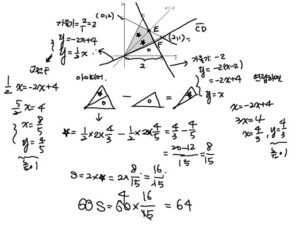
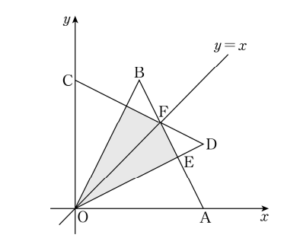
두 직선 \(\mathrm{AB}, \mathrm{OD}\) 의 교점을 \(\mathrm{E}\), 직선 \(\mathrm{AB}\) 와 직선 \(y=x\) 의 교점을 \(\mathrm{F}\) 라 하자. 직선 \(\mathrm{AB}\) 의 방정식은 \(y-0=\frac{2-0}{1-2}(x-2)\) 즉, \(y=-2 x+4\)
이다. 점 \(\mathrm{B}(1,2)\) 를 직선 \(y=x\) 에 대하여 대칭이동한 점 \(\mathrm{D}\) 의 좌표는 \((2,1)\) 이므로
직선 \(\mathrm{OD}\) 의 방정식은 \(y=\frac{1}{2} x\) 이다.
\(-2 x+4=\frac{1}{2} x\) 에서 \(x=\frac{8}{5}\)
\(-2 x+4=x\) 에서 \(x=\frac{4}{3}\)
이므로 두 점 \(\mathrm{E}, \mathrm{F}\) 의 \(x\) 좌표는 각각 \(\frac{8}{5}, \frac{4}{3}\) 이다.
\[
\begin{aligned}
\triangle \mathrm{OAF}: \triangle \mathrm{OEF} & =\overline{\mathrm{AF}}: \overline{\mathrm{EF}} \\
& =\left|2-\frac{4}{3}\right|:\left|\frac{8}{5}-\frac{4}{3}\right| \\
& =5: 2
\end{aligned}
\]
이므로 삼각형 \(\mathrm{OEF}\) 의 넓이는 삼각형 \(\mathrm{OAF}\) 의 넓이
의 \(\frac{2}{5}\) 배이다. 따라서
\(S=\left(\frac{1}{2} \times 2 \times \frac{4}{3}\right) \times \frac{2}{5} \times 2=\frac{16}{15}\) 이므로
\(60 S=64\)
두 직선 \(\mathrm{AB}, \mathrm{OD}\) 의 교점을 \(\mathrm{E}\), 직선 \(\mathrm{AB}\) 와 직선 \(y=x\) 의 교점을 \(\mathrm{F}\) 라 하자.
직선 \(\mathrm{AB}\) 의 방정식은
\(y-0=\frac{2-0}{1-2}(x-2)\) 즉, \(y=-2 x+4\)
이다. 점 \(\mathrm{B}(1,2)\) 를 직선 \(y=x\) 에 대하여 대칭이동한 점 \(\mathrm{D}\) 의 좌표는 \((2,1)\) 이므로
직선 \(\mathrm{OD}\) 의 방정식은 \(y=\frac{1}{2} x\) 이다.
\[
\begin{aligned}
& -2 x+4=\frac{1}{2} x \text { 에서 } x=\frac{8}{5} \\
& -2 x+4=x \text { 에서 } x=\frac{4}{3}
\end{aligned}
\]
이므로 두 점 \(\mathrm{E}, \mathrm{F}\) 의 좌표는 각각
\[
\begin{aligned}
& \mathrm{E}\left(\frac{8}{5}, \frac{4}{5}\right), \mathrm{F}\left(\frac{4}{3}, \frac{4}{3}\right) \\
& \overline{\mathrm{OE}}=\sqrt{\left(\frac{8}{5}\right)^2+\left(\frac{4}{5}\right)^2}=\frac{4 \sqrt{5}}{5} \\
& \overline{\mathrm{EF}}=\sqrt{\left(\frac{4}{3}-\frac{8}{5}\right)^2+\left(\frac{4}{3}-\frac{4}{5}\right)^2}
\end{aligned}
\]
\[
=\sqrt{\left(-\frac{4}{15}\right)^2+\left(\frac{8}{15}\right)^2}=\frac{4 \sqrt{5}}{15}
\]
이때, 두 직선 \(\mathrm{AB}, \mathrm{OD}\) 의 기울기의 곱이 -1 이므로 삼각형 \(\mathrm{OEF}\) 는 직각삼각형이다.
\[
\triangle \mathrm{OEF}=\frac{1}{2} \times \frac{4 \sqrt{5}}{5} \times \frac{4 \sqrt{5}}{15}=\frac{8}{15}
\]
따라서 \(S=\frac{8}{15} \times 2=\frac{16}{15}\) 이므로
\[
60 S=64
\]