1. 다음 식을 계산하시오.
(1) \(\frac{x-1}{x^2-5 x}-\frac{1}{x-5}\)
(2) \(\frac{x^2-4}{x^2-2 x-3} \div \frac{x-2}{x^2-3 x}\)
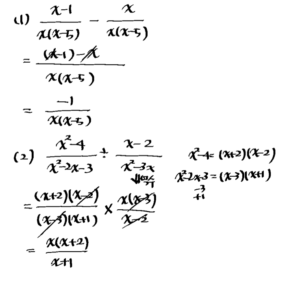
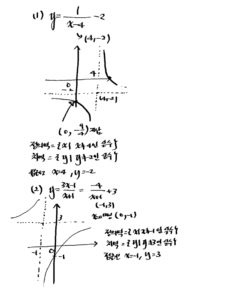
2. 다음 함수의 그래프를 그리고, 정의역과 치역, 점근선을 구하시오.
(1) \(y=\frac{1}{x-4}-2\)
(2) \(y=\frac{3 x-1}{x+1}\)
3. 다음 식을 간단히 하시오.
(1) \((\sqrt{2}-\sqrt{3 x-5})(\sqrt{2}+\sqrt{3 x-5})\)
(2) \(\frac{4}{\sqrt{x+4}-\sqrt{x+2}}\)
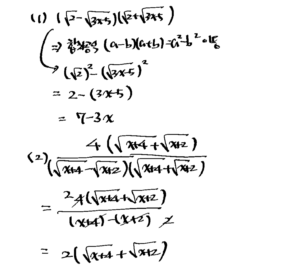
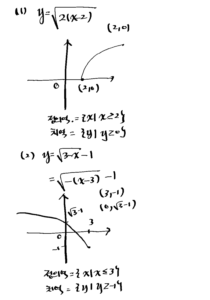
04. 다음 함수의 그래프를 그리고, 정의역과 치역을 구하시오.
(1) \(y=\sqrt{2 x-4}\)
(2) \(y=\sqrt{3-x}-1\)
5. \(x \neq 1\) 인 모든 실수 \(x\) 에 대하여 다음 등식이 항상 성립할 때, 상수 \(a, b\) 에 대하여 \(a b\) 의 값 을 구하시오.
\frac{a}{x-1}+\frac{x+b}{x^2+x+1}=\frac{2 x-5}{x^3-1}[풀이]
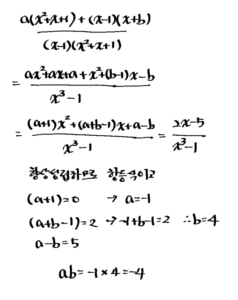
6. 함수 \(y=\frac{2 x+3}{x+1}\) 의 그래프를 \(x\) 축의 방향으로 \(a\) 만큼, \(y\) 축의 방향으로 \(b\) 만큼 평행이동 하 면 함수 \(y=\frac{3 x-2}{x-1}\) 의 그래프와 일치한다고 할 때, 상수 \(a, b\) 의 값을 구하시오.
[풀이]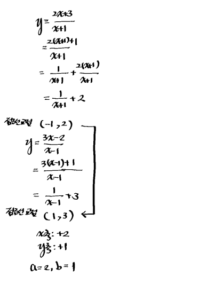
7. 함수 \(y=\frac{a x+b}{x+c}\) 의 그래프가 오른쪽 그림과 같을 때, 상수 \(a, b, c\) 에 대하여 \(a+b+c\) 의 값을 구하시오.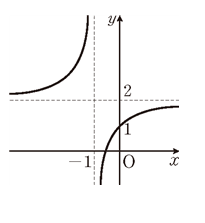
[풀이]
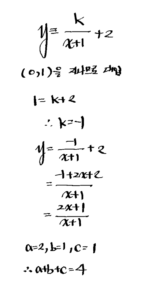
8. 다음 식을 간단히 하시오.
\[
\frac{1}{\sqrt{x}+\sqrt{x+1}}+\frac{1}{\sqrt{x+1}+\sqrt{x+2}}+\frac{1}{\sqrt{x+2}+\sqrt{x+3}}
\]
[풀이]

9. 함수 \(f(x)=\sqrt{-3 x+a}+b\) 의 정의역은 \(\{x \mid x \leq 6\}\) 이고, 치역은 \(\{y \mid y \geq-4\}\) 이다. 이때 \(f(3)\) 의 값을 구하시오. (단, \(a, b\) 는 상수이다.)
[풀이]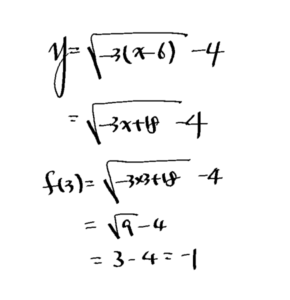
10. 함수 \(f(x)=\sqrt{a x+b}\) 의 그래프와 그 역함수 \(y=f^{-1}(x)\) 의 그래프가 점 \((1,2)\) 에서 만날 때, 상수 \(a, b\) 의 값을 구하시오.
[풀이]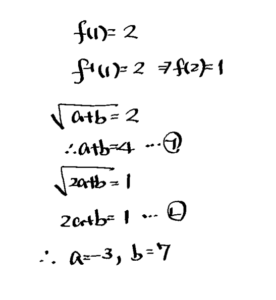
11. 함수 \(y=\sqrt{a x+b}+c\) 의 그래프가 오른쪽 그림과 같을 때, 상수 \(a, b, c\) 에 대하여 \(a^2+b^2+c^2\) 의 값을 구하는 풀이 과정과 답을 쓰시오.
[풀이]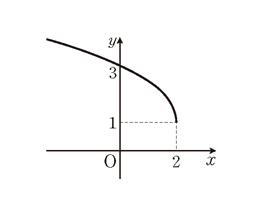
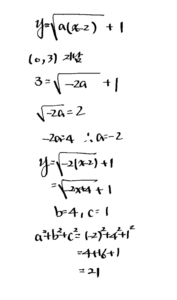
12. 두 함수 \(f(x)=\frac{3 x+5}{2 x-4}, \mathrm{~g}(x)=\frac{a x+b}{c x+d}(a d-b c \neq 0, c \neq 0)\) 일 때, \(x \neq 2, x \neq \frac{3}{2}\) 인 모든 실수 \(x\) 에 대하여 \((f \circ \mathrm{g})(x)=x\) 가 되도록 하는 함수 \(y=\mathrm{g}(x)\) 의 그래프의 점근선을 구하시 오. (단, \(a, b, c, d\) 는 상수이다.)
[풀이]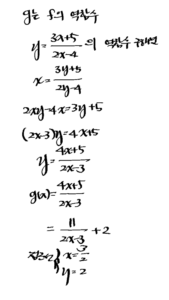
13. 오른쪽 그림과 같이 함수 \(y=\frac{16}{x-1}+2(x>1)\) 의 그래프 위의 점 \(\mathrm{P}\) 에서 두 점근선에 내 린 수선의 발을 각각 \(\mathrm{Q}\) 와 \(\mathrm{R}\) 라 하자. 이때 \(\overline{\mathrm{PQ}}+\overline{\mathrm{PR}}\) 의 최솟값을 구하시오.
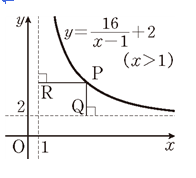
[풀이]
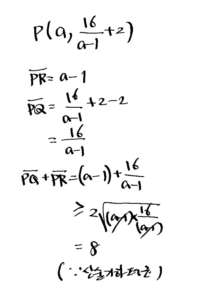
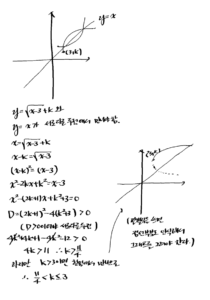
14. 함수 \(f(x)=\sqrt{x-3}+k\) 의 그래프와 그 역함수 \(y=f^{-1}(x)\) 의 그래프가 서로 다른 두 점 에서 만나도록 하는 실수 \(k\) 의 값의 범위를 구하는 풀이 과정과 답을 쓰시오.
[풀이]