도형의 이동 파트는 자체로는 힘들지 않지만, 앞에서 나온 도형에 관한 개념과 공식을 알고 있어야 문제를 해결할 수 있어서 어렵게 느껴집니다.
도형의 이동 문제를 풀기위한 공식들을 정리해 보았습니다.
- 좌표평면 위의 두 점 사이의 거리
좌표평면 위의 두 점 \(\mathrm{A}\left(x_1, y_1\right), \mathrm{B}\left(x_2, y_2\right)\) 사이의 거리
\[
\overline{\mathrm{AB}}=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}
\]
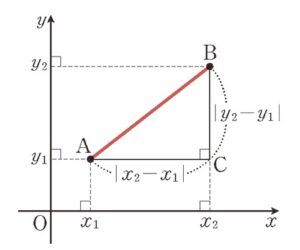
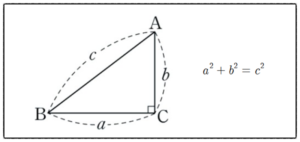
피타고라스의 정리 활용
2. 한 점과 기울기가 주어진 직선의 방정식
점 \(\left(x_1, y_1\right)\) 을 지나고 기울기가 \(m\) 일 때 \(\Rightarrow y-y_1=m\left(x-x_1\right)\)
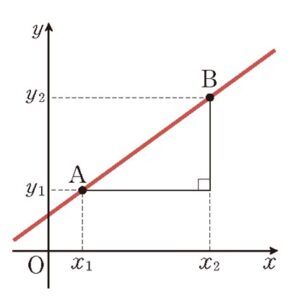
2-1. 두 점이 주어졌을 때 직선의 방정식
\(y-y_1=\large\frac{y_2-y_1}{x_2-x_1}\normalsize\left(x-x_1\right)\)
step1. 먼저 기울기를 구한다.
\(m=\large\frac{y_2-y_1}{x_2-x_1}\)
step2. \(m=\large\frac{y_2-y_1}{x_2-x_1}\)을 \(\normalsize\Rightarrow y-y_1=m\left(x-x_1\right)\)에 대입
3. 점과 직선 사이의 거리
점 \(\left(x_1, y_1\right)\) 과 직선 \(a x+b y+c=0\) 사이의 거리는
\[
\frac{\left|a x_1+b y_1+c\right|}{\sqrt{a^2+b^2}}
\]
4. 원의 방정식
중심의 좌표가 \((a, b)\) 이고 반지름의 길이가 \(r\) 인 원의 방정식은
\[
(x-a)^2+(y-b)^2=r^2
\]
4-1. 원과 직선의 위치관계

반지름의 길이가 \(r\) 인 원의 중심에서 직선까지의 거리를 \(d\) 라 하면
1 서로 다른 두 점에서 만난다. \(\Rightarrow d<r\)
2 한 점에서 만난다. (접한다.) \(\Rightarrow d=r\)
3 만나지 않는다. \(\quad \Rightarrow d>r\)
5. 평행이동
5-1. 점의 평행이동
점 \(\mathrm{P}(x, y)\) 를 \(x\) 축의 방향으로 \(a\) 만큼, \(y\) 축의 방향으로 \(b\) 만큼 평행이동한 점 \(\mathrm{P}^{\prime}\) 의 좌표는 \(\mathrm{P}^{\prime}(x+a, y+b)\) 이다. 즉,
\[
(x, y) \longrightarrow(x+a, y+b)
\]
5-2. 도형의 평행이동
방정식 \(f(x, y)=0\) 이 나타내는 도형을 \(x\) 축의 방향으로 \(a\) 만큼, \(y\) 축의 방향으로 \(b\) 만큼 평행이동한 도형의 방정식은
\[
f(x-a, y-b)=0
\]
\(x\) 대신 \((x-a)\) 대입, \(y\) 대신 \((y-b)\) 대입
6. 대칭이동
6-1. 점의 대칭이동
\begin{array}{ll}
1. x \text { 축에 대한 대칭이동 } & :(x, y) \longrightarrow(x,-y) \\
2. y \text { 축에 대한 대칭이동 } & :(x, y) \longrightarrow(-x, y) \\
3. \text { 원점에 대한 대칭이동 } & :(x, y) \longrightarrow(-x,-y) \\
4. \text { 직선 } y=x \text { 에 대한 대칭이동 }:(x, y) \longrightarrow(y, x)
\end{array}
6-2. 도형의 대칭이동
방정식 \(f(x, y)=0\) 이 나타내는 도형을
1. \(x\) 축에 대하여 대칭이동한 도형의 방정식 : \(f(x,-y)=0\)
2. \(y\) 축에 대하여 대칭이동한 도형의 방정식 : \(f(-x, y)=0\)
3. 원점에 대하여 대칭이동한 도형의 방정식 : \(f(-x,-y)=0\)
4. 직선 \(y=x\) 에 대하여 대칭이동한 도형의 방정식 : \(f(y, x)=0\)
7. 대칭이동을 이용한 거리의 최솟값
좌표평면에서 두 점 \(\mathrm{A}, \mathrm{B}\) 가 직선 \(l\) 에 대하여 같은 쪽에 있고 점 \(\mathrm{P}\) 가 직선 \(l\) 위를 움직일 때, \(\overline{\mathrm{AP}}+\overline{\mathrm{BP}}\) 의 최솟값을 구하는 방법을 알아보자.
